L'objectif est de figurer une lave d'abord liquide et lisse, qui devient peu a peu plus rugeuse, puis au sein de laquelle apparaissent progressivement des ilots plus rigide (ecume solidifiee), lesquels croissent progressivement par aggregation jusqu'a se joindre. Une fois la croute solidifiee, ces ilots apparaissent comme des grosses pierres convoyees par le fleuve de lave profond, lequel fini par s'arreter quand l'epaisseur de la croute rigide empeche tout mouvement (meme si le coeur reste ductile).

  On choisit d'associer un ilot a chaque particule issue de la simulation du mouvement. Comme on l'a dit plus haut, on definit une surface de l'ecoulement simule', sur laquelle on reprojete les particules de la couche externe. Le diagramme de Voronoi de ces points definit les ilots. Un ilot s'appuie alors sur un ensemble de triangles, dont un cote est au centre de l'ilot (i.e. sur une particule de surface) et les deux autres cotes sont au bord.

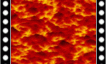
rendu d'un ilot de croute (temps réel)

  Il suffit donc de construire une unique primitive de rendu de lave pour tracer ce triangle. Cette primitive comporte une composante analytique, qui modele le profil ideal d'une pierre (haute au centre, basse au bord), et une composante stochastique figurant la rugosite de surface, obtenue a partir d'un bruit de Perlin. Les parametres de ces deux composantes dependent de la temperature, connue aux sommets (la rugosite augmente avec la viscosite, le profil de la pierre apparrait progressivement). La contrainte est que ces triangles `en relief' doivent se recoller de facon continue derivable, bien qu'ils soient definis dans des reperes differents.

rendu de coulées de lave