![$\displaystyle \sum_p(u_p-g_p)^2+\lambda \left[q_{x,p}(u,g)+q_{y,p}(u,g)\right]$](img/img1.png)
Emmanuel Klein, Thomas OBERLIN
Introduction :
La décomposition d'images multi-échelles est de plus en plus répandue, car elle permet des traitements complexes différents pour chaque échelle. Ces dernières années ont vu l'apparition et l'utilisation massive de filtres gaussiens non linéaires (Non-Linear Gaussian Filters Performing Edge Preserving Diffusion, V. Aurich and J. Weule, Proceedings of the DAGM Symposium, 1995). Notamment, de nombreuses recherches ont été menées sur le filtre bilatéral (Bilateral Filtering for Gray and Color Images, C. Tomasi and R. Manduchi, Proceedings of the international Conference on Computer Vision, 1998). Cependant, si les qualités du filtre bilatéral sont indéniables, notamment sa capacité à préserver les discontinuités de l'image, il crée des artefacts, principalement des halos autour des zones discontinues.
Nous allons ici étudier un nouveau filtre non-linéaire préservant les bords, introduit par Farbman et. al en 2007, qui pallie à certains défauts du filtre bilatéral, tout en étant également très performant. Le travail a d'abord consisté en une implémentation C++ du filtre. Nous l'avons alors expérimenté sur plusieurs applications importantes, notamment le tone-management pour un travail photographique, ou encore la stylisation d'images et de vidéo.
Il s'agit de transformer l'image d'entrée en une image proche, la plus lisse possible sauf autour de valeurs significatives du gradient. Soit l'image d'entrée g, on va donc calculer l'image u qui minimise la quantité :
![$\displaystyle \sum_p(u_p-g_p)^2+\lambda \left[q_{x,p}(u,g)+q_{y,p}(u,g)\right]$](img/img1.png)
, où les termes ![]() et
et ![]() sont quadratiques en u, et prennent en compte les dérivées de u et g selon l'axe des x et des y. Le filtre WLS pose :
sont quadratiques en u, et prennent en compte les dérivées de u et g selon l'axe des x et des y. Le filtre WLS pose :
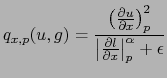
l étant la log-luminance de l'image g. ![]() et
et ![]() sont les paramètres du filtre, nous allons voir leur influence.
sont les paramètres du filtre, nous allons voir leur influence.
On voit donc que l'importance donnée au terme de discontinuité en x est inversement proportionnel à la discontinuité de la log-luminance (qui se rapproche de notre perception visuelle des contours d'une image). Pour les pixels p où l'image est lisse, ce dernier terme devient prépondérant. Inversement, autour d'un contours, ce terme devient négligeable, et u se rapprochera très fortement de g. Le paramètre epsilon évite d'avoir des valeurs infinies pour une portion d'image constante, sa valeur est typiquement 0.00001.
On définit de même le terme de discontinuité selon y :
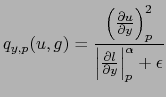
En notations matricielles, notant Dx et Dy des opérateurs différentiels, on obtient l'écriture suivante :
Où ![]() et
et ![]() sont des opérateurs différentiels discrets (matrices bi-diagonales). Enfin, en posant
sont des opérateurs différentiels discrets (matrices bi-diagonales). Enfin, en posant
![]() , il s'agit de résoudre le système suivant :
, il s'agit de résoudre le système suivant :
On est donc ramené à résoudre un système linéaire creux, puisque la matrice ![]() est penta-diagonale. Pour l'implémentation, on aura utilisé la formule suivante, plus simple :
est penta-diagonale. Pour l'implémentation, on aura utilisé la formule suivante, plus simple :
L'idée ici est de construire une pyramide d'images de plus en plus lisses, ce qui donnera une décomposition multi-échelle. En considérant l'image à peu près constante, l'opérateur ![]() devient un Laplacien homogène, à une constante près. Dès lors, lorsqu'on multiplie
devient un Laplacien homogène, à une constante près. Dès lors, lorsqu'on multiplie ![]() par une constante
par une constante ![]() , on monte d'un facteur
, on monte d'un facteur ![]() dans le domaine des fréquences.
dans le domaine des fréquences.
Pour obtenir une pyramide, on va donc itérer le filtre sur l'image, en multipliant à chaque fois ![]() par un facteur
par un facteur ![]() . On obtiendra alors les versions de plus en plus filtrées
. On obtiendra alors les versions de plus en plus filtrées
![]() de
de ![]() , où
, où ![]() et :
et :
On obtient parallèlement les couches successives de détail
![]() .
.
Présentons d'abord le filtrage WLS, et montrons l'influence des paramètres.
Les figures suivantes montre deux décompositions de la même image, pour des paramètres différents.
Grâce à cette décomposition, on peut aisément augmenter les détails à n'importe quelle échelle. Il suffit, dans notre décomposition
![]() , de pondérer les échelles
, de pondérer les échelles ![]() . Nous avons principalement travaillé sur des décompositions 2 échelles, nous allons présenter ici nos principaux résultats.
. Nous avons principalement travaillé sur des décompositions 2 échelles, nous allons présenter ici nos principaux résultats.
La figure qui suit montre plusieurs reconstructions de l'image originale à partir de la pyramide des décompositions. Les détails sont fortement exagérés et peuvent paraitre artificiels, mais cela montre le très bon comportement du filtre WLS : on n'obtient pas d'artefacts comme des halos lumineux.




|
Les paramètres ont ici aussi toute leur importance : on présente ici leur influence, en montrant la même image recombinée obtenue à partir de pyramides de décomposition différentes. On observe que pour des paramètres trop élevés, le filtrage est grossier, et les détails augmentés sont de moins en moins fin. Par ailleurs, on observe un halo lumineux parasite.
-->
![]() , le paramètre
, le paramètre ![]() valant toujours
valant toujours ![]() .
.






Cette reconstruction est une des plus simples possible, il existe de nombreuses façons de l'améliorer, pour un rendu plus réaliste notamment. Une de ces façons consiste à augmenter les détails en fonction de l'éloignement à la prise de vue : les éléments du premier plan seront bien plus détaillés, ce qui améliore la perception de la profondeur, et donne une image plus réaliste; Notons que l'inverse est possible également, pour des effets stylistiques.
La figure suivante montre l'utilisation de ce procédé. On a utilisé une décomposition deux échelles, en forçant les détails fins au premier plan, et les détails grossier à l'arrière-plan. Concrètement, cela revient à multiplier le mode ![]() par la carte de profondeur, et le mode
par la carte de profondeur, et le mode ![]() par son inverse. La différence est surtout nette entre les deux dernières images : dans la recomposition inversée, on accentue les détails grossiers, ce qui crée des artefacts autour des feuilles, alors que les briques, au fond, sont très détaillées.
par son inverse. La différence est surtout nette entre les deux dernières images : dans la recomposition inversée, on accentue les détails grossiers, ce qui crée des artefacts autour des feuilles, alors que les briques, au fond, sont très détaillées.




|
On peut accentuer cet effet stylistique en quantifiant la carte de profondeur au lieu d'utiliser une profondeur continue. Dans le filtrage WLS, on modifie alors les paramètres selon le plan de l'image considéré. Cette technique est plus aprofondie dans la partie suivante, on donne néanmoins un exemple d'utilisation :

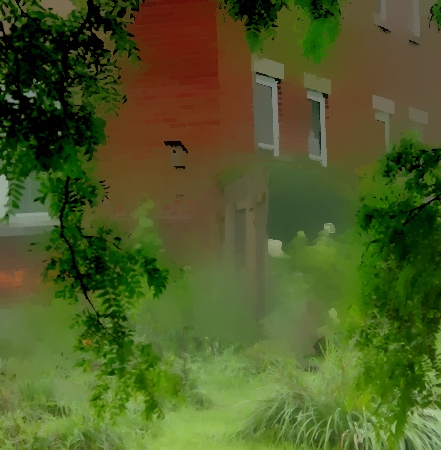

|
Nous ne rappelons pas ici le principe du filtre bilatéral, on pourra pour cela se référer au site de S. Paris. Ce filtre, non-linéaire et préservant également les contours, a été beaucoup étudié et a donné lieu à de nombreuses application. Nous allons ici comparer les résultats donnés par les deux filtres, pour le Tone-Management sur différentes images.



|
L'un des principaux avantages du fitre WLS est de respecter les bords avec soin. L'idée qui en vient est d'utiliser les filtre WLS pour styliser des photos, en aplanissant les couleurs et ne gardant que les contours principaux.
Ici nous travaillons sur une image préalablement filtrée par l'algorithme WLS. Nous commençons par convertir l'image à un autre format que RGB : le format Lab, qui est supposé respecter davantage la sensibilité de l'oeil humain. En effet nous sommes plus sensibles aux changements de luminosité que des couleurs RGB.
Sur cette image nous appliquons 2 traitements en parallèle :
Detection des contours
Nous appliquons à l'image l'algorithme de sobel : les gradians horizontaux sont detetés par convolutions de l'image par la matrice Dx :
+1 0 -1 +2 0 -2 +1 0 -1les gradians verticaux par convolution avec la matrice Dy :
+1 +2 +1 0 0 0 -1 -2 -1L'image des bords est obtenue en prenant la norme des 2 gradians, et en supprimant les bords de faibles intensités (qui correspondent à de faibles gradians).
Quantification des couleurs
En parallèle nous quantifions sur l'image la luminance, pous un effet plus cartoon.
Le résultat est une image cartoon qui ne semble pas provenir d'une photo.
Utilisation des cartes de profondeurs
Nous pouvons aussi utiliser les cartes de profondeur afin de permettre un effet cartoon plus fidèle.
En effet, il est courant que les dessinateurs dessinent le premier plan en détail, alors que l'arrière plan est dessiné grossièrement.
L'idée est d'appliquer diffentes valeures du filtre WLS sur une image, selon la profondeur estimée des éléments.
Dans nos exemples nous utilisons 3 échelles, ou la première ne subit qu'un léger filtrage alors que la dernière ne garde que les formes générales. Pour pouvoir distinguer ces 3 zones nous quantifions la carte de profondeur. Nous appliquons 3 filtrages sucessifs à l'image et calculons deux masques qui correspondent à la différence entre le premier filtre et les deux autres. Nous multiplions ensuite ces masques par la zone correspondante (1 si le pixel appartiens à la zone, 0 sinon). Enfin nous calculons la somme de l'image avec les 2 masques.
Nous pouvons aussi créer la carte de manière artificielle : soit pour pallier à une absence de carte, soit pour créer un effet de style. On voudra par exemple mettre en valeur un objet au milieu de l'image, en omettant le premier plan.



|



|
Conclusion
On a présenté ici la décomposition modale empirique, ses motivations, ses qualités, en insistant sur son gros inconvénient : l'absence de formalisme et un temps de calcul important.