Projet Image 2007
Remaillage semi-régulier par chartification
DU Xia, RONNAS Staffan, WOLFF Martin
Sommaire
Introduction
Le but du projet était d'implementer une algorithme de remaillage proposé par Igor Guskov dans son papier Manifold-Based Approach to Semi-Regular Remeshing. Cette page est un présentation de notre travail : une déscription de notre compréhension de l'algorithme, un bilan des résultats que nous avons obtenus et une résumé de nos impressions du projet.
Malheureuesement, nous avons pas réussi à finir à implémenter tout l'algorithme dans le temps donné, ce qui fait que ce rapport est incomplet au niveau de résultats. Nous présentons quand même dans l'intérêt de complétude notre idée de comment la reste de l'algorithme fonctionnerait.
Description de l'algorithme
L'algorithme se divisent en cinq étapes, décrits plus en détail ci-dessous. D'abord on partitionne le maillage donné en grandes régions (tiles) avec l'algorithme de chartification. A partir de cette division, un maillage très simplifié appelé le maillage de base est créé. Avec ce maillage de base on construit une paramétrisation initiale du maillage de départ, qui est ensuite optimisée. Finalement, on obtient un maillage semi-régulier en raffinant le maillage de base.
Chartification
La chartification se fait itérativement. On commence avec un ensemble des sommets du maillage (appelés "germes") pris au hasard. En utilisant ces germes une diagramme de Voronoi est créée, c'est à dire on partitionne les sommets en régions selon leurs distances aux germes. Puis on regarde si certaines conditions sont vérifiés qui servent à assurer que le maillage de base créé à partir de ces régions aura des bonnes propriétés pour donner un maillage de résultat semi-régulier. Dès que l'on trouve une condition qui n'est pas vérifiée, on ajoute une germe, on effectue un répositionnement des germes existants, et on calcul à nouveau la partition.
Etant donné un ensemble des germes, on partitionne les autres sommets du maillage en régions, "Voronoi tiles", en utilisant une géneralisation de l'algorithme de Dijkstra avec plusieurs sommets de départ. Pour cela une file de priorité est utilisée. La priorité est définie comme la distance du sommet à la germe la plus proche. Tant que la file n'est pas vide, on sort le premier élément et on l'ajoute au tile le plus proche. Ensuite on ajoute ses voisins dans la file, où on met à jour leurs priorités s'ils y existent déjà. L'algorithme se termine quand il n'y a plus d'élément dans la file qui implique que chaque sommet est associé à la germe la plus proche.
Les conditions à vérifier sont les suivants :
- "Encrouched boundaries (EB)" : Si un tile touche la frontière d'un maillage contenant des trous, la germe doit être un des sommets de cette frontière. Cette condition est vérifiée en parcourant les tiles avec des trous en créant une nouvelle germe sur la frontière si l'existant n'y se trouve pas.
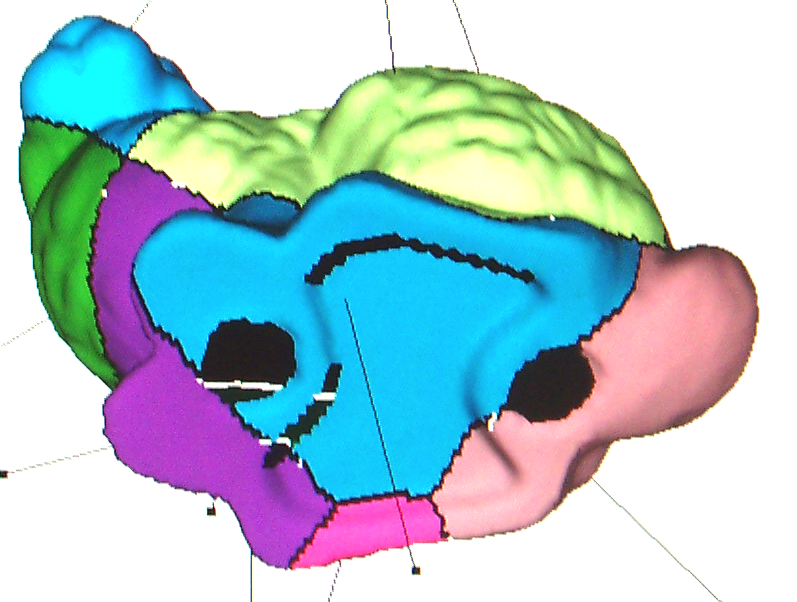
Fig. 1. Le tile turquoise touche la frontière du maillage, mais sa germe n'y se trouve pas.
- "Non-zero genus (NZ)" : Le genus de chaque tile doit être 0. Afin de vérifier cette condition, un parcours des sommets sur la frontière du maillage est effectué. Si l'on trouve une cirucit des sommets sur la frontière qui est contenue dans le tile, le genus n'est pas zéro, et on ajoute une germe adjacent à l'ancienne germe.
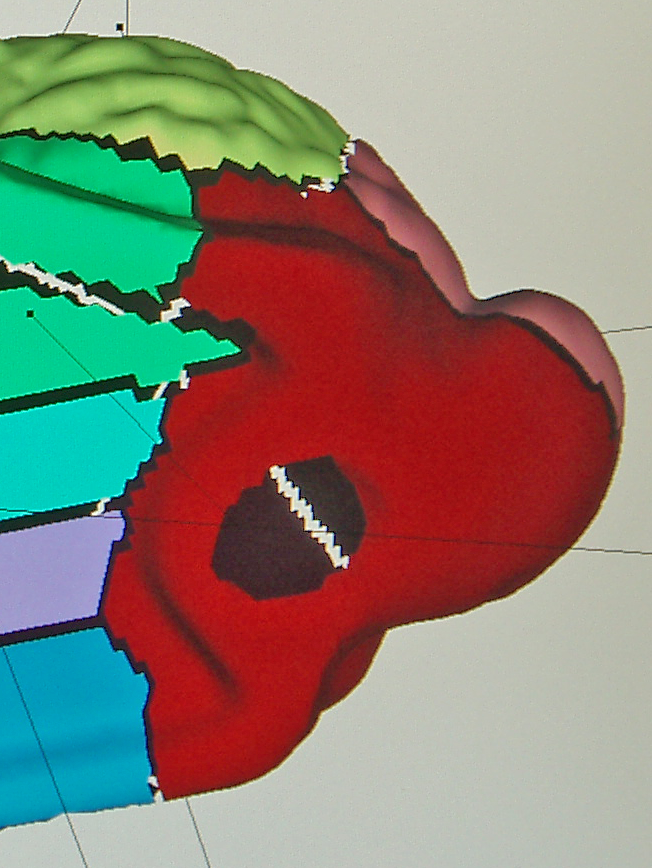
Fig. 2. Le tile rouge a un trou à l'intérieur - son genus est 1.
- "Multiple tile boundary components (MB)" : Le frontière d'un tile avec ses voisins doit consister en un seule component connexe. Pour vérifier cette condition, on prend un sommet qui a un voisin dans un autre tile (un sommet "sur la frontière de la région"), et on parcourt récursivement ses voisins qui se trouvent eux-même sur la frontière. Dans cette façon, on visite toute le component connexe contenant le sommet de départ. Si on trouve qu'on a parcouru tout les sommets qui forment la frontière de ce tile, la condition est vérifiée. Sinon, on ajoute comme nouvelle germe un sommet voisin de l'ancienne.

Fig. 3. Le frontière du tile vert consiste en deux courbes qui ne sont pas connexe - une courbe sur le pied de Homer et un sur son ceinture.
- "Single curve tile boundaries (SC)" : Un tile ne doit avoir plus qu'un tile voisin sur chaque courbe de la frontière. De ce que nous avons compris, cette condition devrait toujours être vérifiée, alors on ne la vérifie pas explictement dans le code.
- "Multiple neighbour instances (MN)" : La partie de la frontière entre deux tiles doit être connexe. La vérification de cette condition consiste en d'abord groupant les sommets sur le frontière de chaque tile selon les tiles dans lesquels ils ont des voisins. Ensuite pour chaque groupe, on commence avec un sommet et on trouve une chaîne des sommets connectés à celui-ci. Si cette chaîne ne contient pas tous les sommets du groupe, on a trouvé une violation de la condition, et on ajout comme nouvelle germe un des sommets avec un voisin adjacent de la plus court des courbes frontières avec le tile concerné. En effet, comme les longeurs des courbes frontières est assez compliqué à calculer, une approximation est faite : on calcul les longeurs de deux components connexes des sommets au lieu de la "vraie" longeur de la frontière.

Fig. 4. La frontière entre le tile vert clair et le tile violet n'est pas connexe - le tile bleu est au milieu.
- Aire et courbure limités : l'aire et la courbure des tiles ne doivent pas être trop grands. Pour vérifier cela une variance des vecteurs normales avec les aires des triangles comme poids est calculée pour chaque région. Le calcul entraine parcourir toutes les faces du tile en sommant le produit de ces aires et la difference entre leurs vecteurs normals et la moyenne des vecteurs normals pour toute la région. Si la variance est supérieur à un seuil spécifié par l'utilisateur, une nouvelle germe et choisie entre les sommets adjacents à la germe existante.
Le repositionnement des germes consiste simplement en remplacer chaque germe qui ne se trouve pas sur la frontière du maillage par le sommet du tile le plus proche à son barycentre.
Création du maillage de base
Le maillage de base est crée à partir des tiles calculés dans l'étape de chartification. En effet, le maillage de base est la duale de l'ensemble des tiles Voronoi sur le maillage de départ. Autrement dit, on peut le créer en associant un sommet à chaque région et en créant une arrête entre deux sommets si leurs tiles sont voisins. On choisit naturellement comme sommets du maillage de base les germes des tiles.
En utilisant OpenMesh la réalisation est dans ce cas un peu plus compliquée que la théorie. Pour créer un maillage avec OpenMesh, il faut spécifier les faces (pas les arrêtes). Une face est spécifiée par un cycle de sommets et l'oriéntation d'une telle cycle, ce qui rend la création du maillage de base plus difficile. Le problème est qu'il est possible de créer deux faces entre la même suite de noeuds si leurs oriéntations sont opposés, mais au même temps il est impossible de créer deux faces adjacentes ayant d'oriéntations opposés.
La solution que nous avons utilisé est d'ajouter tous les germes des tiles au maillage de base et les parcourir en profondeur d'abord afin d'assurer la création des faces côte à côte. Ensuite pour chaque sommet b, on crée les faces dans le même ordre dans la région Ωb des faces adjacentes au sommet b et marque les sommets parcourus pour éviter la création d'une même face plusieurs fois. Afin d'éviter de créer la face incorrectes dans la région Ωb, on utilise une liste ordonnée des sommets voisins du sommets b, ce qui permette de créer les faces côte à côte. De plus, le premier sommet entré doit être une germe qui a déjà été parcouru s'il y en a. Pour les maillages contenant des trous, on ne créer pas les faces entre deux sommets qui sont sur le bord du même trou.

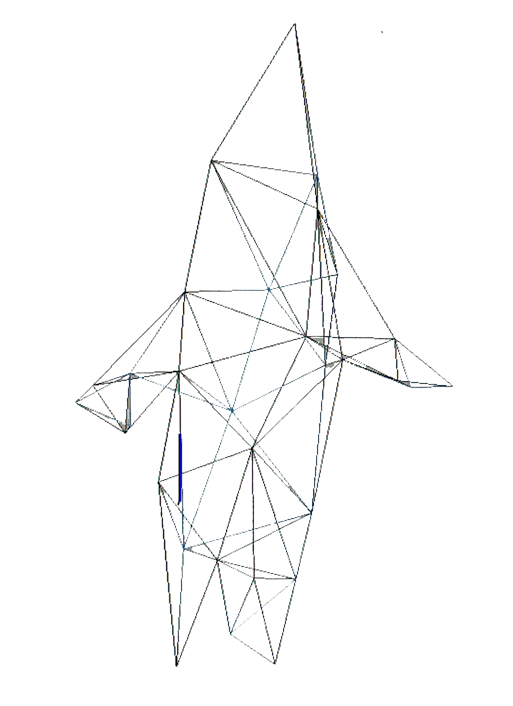
Fig. 5. Maillage de base de Homer
Création de la paramétrisation initiale
Afin de retenir les caractéristiques du maillage de départ dans la reconstruction de celui-ci, on crée une paramétrisation. Ceci entraine associer à chaque sommet du maillage de départ un point dans un atlas de carte de R^2. Après avoir crée une paramétrisation initiale, celle-ci est optimisée en minimisant une fonction d'energie.
La paramétrisation initiale est calculée en utilisant des coordonnées moyennes ("Mean value coordinates"). Ces coordonnées permettent d'exprimer un point dans une polygone comme une combinaision affine des coins de la polygone. En genéralisant directement le calcul en trois dimensions, on peut ainsi exprimer chaque sommet dans le maillage de départ comme une combinaison affine de ses voisins. Les points dans R^2 associés aux sommets sont déterminés en imposant que chaque point peut être exprimé comme la même combinaison des points voisins. Ceci donne un système linéaire à résoudre.
Pour que ce système ait une solution unique, il faut imposer des conditions aux limites, c'est-à-dire spécifier les points dans R^2 associés aux points sur la frontière de chaque tile du maillage de départ. Pour detérminer ces conditions aux limites, on passe par le maillage de base, en postulant que les courbes frontières des tiles de Voronoi sur le maillage de départ corréspondent aux frontières de tiles de Voronoi sur le maillage de base. Ces dernières sont simplement des droites passant par les barycentres des faces et mi-points des arrêtes du maillage de base.
Ensuite on introduit ce que Guskov appelle une structure différentielle sur le maillage de base. Il s'agit d'un ensemble d'applications (ou chartes) R_b, un pour chaque sommet b du maillage de base, de faces autour le sommet vers R^2. Ces applications, appelés "polaires" entraine le calcul des coordonnées barycentric et des fonctions complexe. En utilisant ces applications, on trouve les points dans R^2 qui correspondent aux points sur le frontière des tiles dans le maillage de départ, ce qui permet de résoudre le système pour les autres points. (Réference : Floater, Parametrization and smooth approximation of surface triangulations
Dans l'implementation, on parcours les tiles et assemble pour chaque tile la matrice du système en parcourant les sommets du tile. Pour les sommets sans voisins dans des autres tiles, les coordonnées moyennes par rapport aux sommets voisins sont calculées et stockées dans la matrice. Les sommets restants sont parcourus séperament. Pour chaque sommet, on doit maintenant d'abord calculer les points sur la frontière avec les autres tiles. Ensuite, on peut calculer les coordonnées moyennes du sommet par rapport à ses voisins (qui comprises maintenant des autres sommets et les points sur la frontière), et le stocker dans la matrice. Après, on calcule les points dans R^2 correspondant aux points sur la frontière comme décrit ci-dessus. Ces points permettent de créer le second membre du système.
Comme chaque tile peut contenir un nombre assez important des sommets, chacun seulement liés à un petit nombre des autres sommets, la matrice sera creuse, mais n'aura pas des autres bonnes propriétés comme être symétrique ou défini positive. En vue de ces conditions, nous utilisons un solveur de gradients bi-conjugées (BiCGstab) (l'implementation utilisée peut être trouvée ici) qui est basé sur la bibliothèque BLAS. Pour le stockage de matrice, nous avons crée notre propre type qui évite la stockage des zéros.
Optimisation de la paramétrisation
Afin d'arriver à un maillage semi-régulier, il faut que la paramétrisation utilisée dans la reconstructuion soit assez lisse. La paramétrisation initiale ne prend en compte que les rélations entre les sommets du maillage de départ à l'intérieur de chaque tile. Cette paramétrisation doit être modifiée pour améliorer sa continuité. Guskov propose de faire cette modification de sorte qu'une certain fonction d'energie soit minimisée. La fonction est en bréf une somme des erreurs entre le point dans R^2 associé à un sommet dans le maillage de départ et la combinaison des points voisins avec des coordonnées moyennes du sommet par rapport à ses voisins. Le somme porte sur tout les sommets du maillage de départ avec tout les applications R_b possibles et utilise comme poids l'aire associé au sommet et la même fonction spline utilisé dans la reconstruction du mailage.
Cette fonction est trop compliqué à optimiser sur tout le maillage dans un coup, ainsi Guskov identifie deux types de régions sur le maillage de base qui se prêtent à une optimisation par partie. D'abord, on parcours les arrêts du maillage de base et on considère le région qui consiste des deux faces adjacents. Comme ce région est assez compliqué, il faut d'abord faire une transformation des points de la paramétrisation et de la fonction à minimiser. Après avoir fait cette transformation, une bibliothèque d'optimisation qui fourni un methode de quasi-Newton (L-BFGS) est utilisée pour trouver la configuration des points de la paramétrisation qui minimise la fonction. L'appel à cette bibliothèque exige la définition d'un méthode qui calcule la valeur de la fonction et son gradient à partir d'une configuration des points donné. Comme point de départ on utilise pour la première arrêt la paramétrisation initiale crée dans l'étape précédent et ensuite les dernières points obtenus dans l'optimisation. En optimisant chaque région, seulement les sommets qui ont tout ces voisins dans la région seront modifiés. A l'autre côté, chaque sommet appartient à plusieur régions et sera ainsi modifié plusieurs fois.
Après avoir optimisé avec les régions associés aux arrêts, on continue avec des régions assoicés aux vertices. Pour chaque sommet dans le maillage de base, on considère la région des points qui sont plus proche au sommet que un certain seuil, choisi tel que la fonction à optimiser se simplifie beaucoup. Effectivement, le problème d'optimisation se réduit à calculer la paramétrisation avec le methode utilisé quand la paramétrisation intiale était crée. On trouve ainsi les sommets dans le maillage de départ dont le sommet correspondant sur le maillage de base est dans la région. Pour tout les sommets qui ont tout leurs voisins aussi à l'intérieur du région, on calcule les coordonnées moyennes. Les sommets restants ne peuvent pas être modifiés pendant l'optimisation et leurs paramétrisations courants sont utilisés comme conditions aux limites. On assemble le système linéaire et on le résout dans la même manière que precedemment. La paramétrisation est mis à jour avec la solution pour les sommets qui ont tout leurs voisins à l'intérieur du région.
Reconstruction du maillage
La reconstruction du maillage est faite en deux étapes. D'abord, on sous-divise le maillage de base en divisant chaque triangle en 4 ("1-4 split") récursivement un certain nombre des fois, ce que nous donne un ensemble des sommets s sur le maillage de base. On applique ensuite une des applications R_b de la structure différentielle du maillage de base pour obtenir un point dans R^2. On trouve ensuite le point sur le maillage de départ correspondant, en utilisant des coordonnées barycentriques. Effectivement, on trouve le triangle des points dans R^2 dans lequel R_b(s) se trouve et on calcule les coordonnées barycentrique de R_b(s) par rapport à ces points. Pour retrouver le point dans le maillage de départ on calcule le combinaison affine des sommets correspondants aux points de la triangle avec les coordonnées barycentriques.
Or, comme les domaines de définition des applications R_b se chevauchent, il y en a normalement plusieurs qui peuvent être utilisés pour l'application vers R^2. Afin de prendre en compte tout ces possibilités, une moyenne des points reconstruit sur le maillage de départ est calculée. Cette moyenne utilise comme poids une fonction spline cubique de la distance entre s et le sommet de maillage de base b.
Implementation
L'algorithme de Guskov
Nous avons commenté notre implémentation de l'algorithme de Guskov avec doxygen. Pour accéder la page web du documentation de notre implémentation veuillez suivre ce lien.
L'interface
Nous avons crée une interface graphique pour exécuter les différents étapes de l'algorithme à partir de l'interface de base fournie. Dans cette programme nous avons ajouté la possibilité de créer une distribution initiale des germes et créer une chartification. C'est aussi possible de spécifier les différents paramètres de l'algorithme, notamment le nombre des germes de départ, le nombre des sous-divisions du maillage de base utilisé dans la reconstruction, et les constants qui entrent dans les formules mathématiques des différents étapes de l'algorithme. Pour bien pouvoir visualiser la chartification, le programme donne chaque face du maillage un couleur indiquant le tile auquel il appartient. Une légende pour cette coloriage est aussi affichée. De plus, les germes de chaque tile peuvent être affichés.
Il reste encore beaucoup à faire sur l'interface. Nous avons surtout essayé d'implementer l'algorithme de Guskov, ce qui a pris plus de temps que prévu. Comme nous n'avons pas parvenu à le finir, l'interface n'est pas très développé.
Résultats
Comme nous n'avons pas réussi à implementer toute l'algorithme, les résultats qui suivent ne porte que sur les étapes de la chartification et la création du maillage de base et la paramétrisation.
La chartification donne un résultat qui est correct au sens que l'ensemble des tiles obtenus satisfont les conditions, ce qui permette de créer un maillage de base après. Par contre, le nombre de tiles, et ainsi la durée d'éxecution de cette étape, varie grandement entre les éxecutions. Parfois, une chartification satisfaisant et trouvé presque tout de suite, autrefois la vérification des conditions peut créer un grand nombre des tiles. Comme le résultat dépend de la distribution initiale des germes, qui est aléatoire, c'est difficile de contrôler le résultat finale et le temps d'éxecution. Ce dernier peut de temps en temps atteindre plusieurs minutes pour les grands maillages. Nous avons essayer de voir comment le nombre de tiles résultat varie comme fonction de nombre des tiles de départ. Fig. 6 montre le résultat pour le maillage Homer. Pour les maillages plus compléxes le nombre de tiles résultat étaient trop grand pour pouvoir faire des statistiques dans une manière efficace.
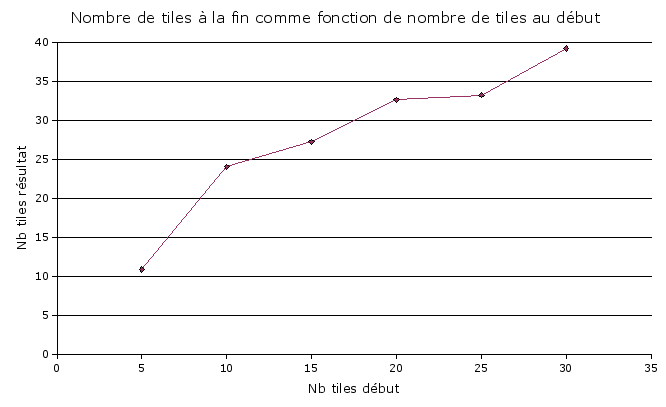
Fig. 6 La variation de nombre de tiles résultat comme fonction de nombre de tiles de départ pour Homer. Chaque point est un moyenne sur 10 distributions initiales différents.
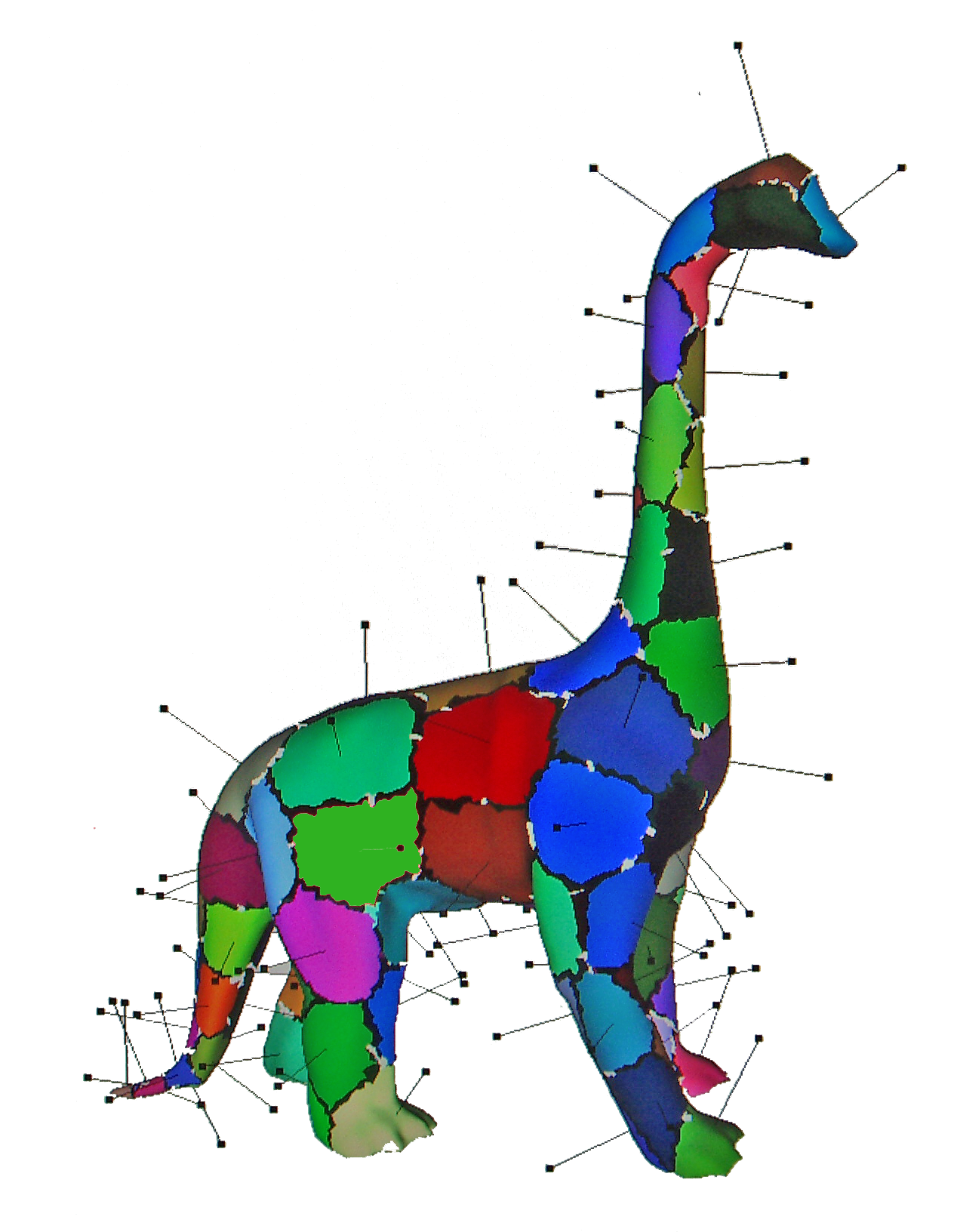
Fig. 7 Une chartification de Dino avec un grand nombre de tiles.
Pour pouvoir mieux contrôler le résultat final, il aurait été bon de permettre l'utilisateur de modifier la distribution initiale dans l'interface avant commencer la chartification, même si cela contredira un peu l'idée de l'algorithme qui selon Guskov est de ne pas exiger d'intervention humaine. Malheureusement, la myriade de problèmes rencontrée dans l'implementation de l'algorithme nous a empêcher de améliorer l'interface encore plus.
C'est surtout avec les maillages contenant des trous que nous avons vu que notre recherche d'une bonne chartification n'est pas toujours efficace. Effectivement, le programme à tendence de créer trop des petits tiles quand il y a un tile qui touche plusieurs trous. Une idée pour se débarrasser cette condition serait d'imposer une borne inférieur du nombre des vertices dans un tile et supprimer des germes qui les tiles deviennent trop petits. Il faudrait dans ce cas faire attention de assurer la bonne convergence du methode.
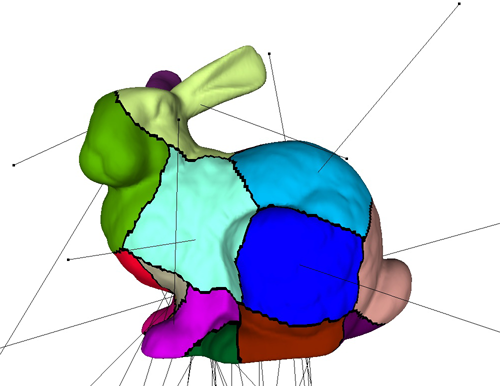
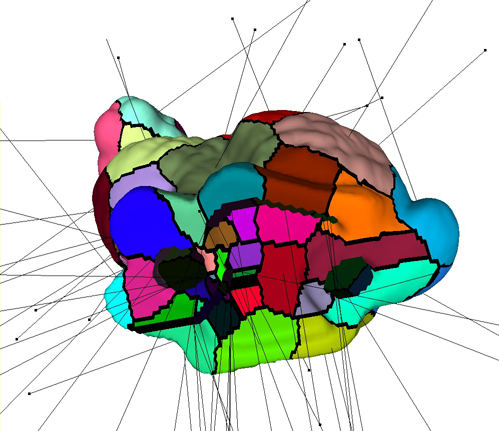
Fig. 8. Le maillage marche souvent mieux dans les régions sans trous (gauche) que là où il y a des trous (droite).
La création du maillage de base semble marcher bien. Les résultats corresponds à ce que on s'attend. Le problème est que ils sont parfois un peu trop détaillés pour permettre un calcul rapide de la paramétrisation, mais ceci est la conséquence d'un grand nombre de tiles dans la chartification.

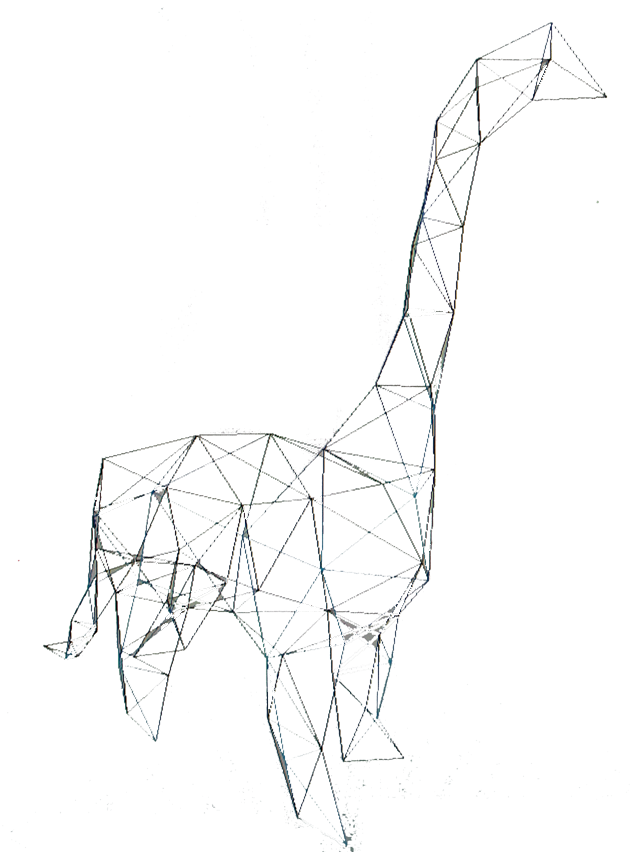
Fig. 9. La construction du maillage de base marche bien sont trop détaillés dans les cas où la chartification a créé trop de tiles.
Nous avons aussi mésuré le temps de calcul, avec le maillage Homer. Pour ce maillage la chartification fonctionne bien, et on a une croissance linéaire avec le temps. C'est intéressant de voir que le calcul de la paramétrisation initiale décroit legèrement avec le nombre de tiles, ce que nous pensons est due au fait que les systèmes linéaires résolus sont plus petits, ce qui donne une convergence plus rapide. L'étape de reconstruction (resampling) est dominant, mais comme cette étape n'est pas mise au point, ce n'est pas très intéressant de le comparer avec les autres. Pour les autres maillages le temps de calcul de la chartification est beaucoup plus important due au grand nombre de tiles qui sont souvent crées.
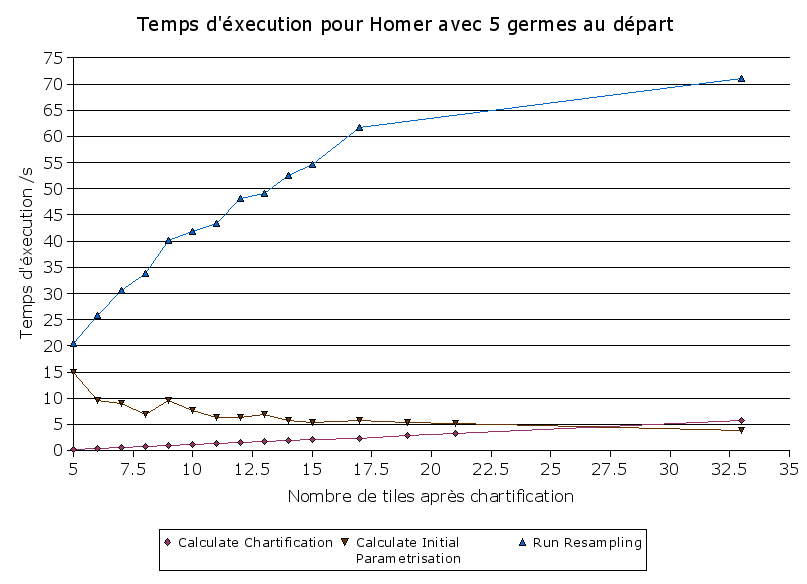
Fig. 10 Le temps d'éxecution des différents étapes avec le maillage Homer.
Nous avons implementé les étapes de la création et de la paramétrisation initiale et la reconstruction du maillage, mais nous n'avons pas obtenu de résultats satisfaisants. Nous pensons que la faute se trouve dans le code de reconstruction, et que la paramétrisation est correcte (voir Fig. 11). Cependant, nous n'avons pas pu tester les deux étapes séparament. Le premier pas de la reconstruction, la sous-division, fonctionne correctement. Pour l'étape d'optimisation nous n'avons fait qu'une squelette de l'implémentation.

Fig. 11. Dino après la sous-division.
Impressions sur le projet
Même si nous sommes déçus de ne pas avoir parvenu à finir implémenter tout l'algorithme, nous avons trouvé le projet très intéressant. Il nous a permis d'apprendre les idées de base du sujet de maillages et les algorithmes associés, dont nous ne connaissions pas avant. Se plonger dans un problème tout nouveau et assez complexe a été stimulant mais aussi parfois frustrant. Nous avons dû chercher des informations et clarifications dans des papiers scientifiques où le contexte des problèmes traités était souvent implicite, et non pas toujours le bon pour nos questions.
A notre avis la raison de notre échec de finir le projet se trouve surtout dans son complexité et notre manque d'expérience du sujet. Nous avons plusieurs fois pensé avoir trouvé une solution à un problème, et, seulement après avoir l'implementé (et deboggé), découvert que notre idée était totalement erronée. L'exemple la plus évident était notre méprise pour le calcul de la paramétrisation initiale. En recul, c'est clair que nous aurions dû poser plus de questions et chercher plus d'aide quand nous avions de problèmes.
La bibliothèque que nous avons utilisé pour la traitement des maillages, OpenMesh, était un grand aide dans le travail. Nous l'avons trouvé assez intuitive et facile à comprendre et utiliser, même si son documentation laisse beaucoup à désirer. Seulement les méthodes de création des maillages nous resemblait un peu compliqués. Aussi, les methodes fournis par OpenMesh sont d'assez bas niveau : il n'existe pas par exemple quelque chose qui permet de chercher l'arrêt entre deux sommets. Nous aurions peut-être du nous-même écrire une module avec des fonctions auxiliaire pour faire des choses récurrents comme cela pour simplifier notre code.
Layout de cette page web utilise le stylesheet de l'équipe "Antoine MELER & Adrien BERNHARDT" de l'année 2006.
top
Grenoble, le 15 juin 2007













