Sujet de Master 2007-2008

Reconstruction virtuelle temporellement cohérente d'animaux en mouvement
Virtual, temporally coherent reconstruction of moving animals

Extrait d'une vidéo d'un rat en mouvement
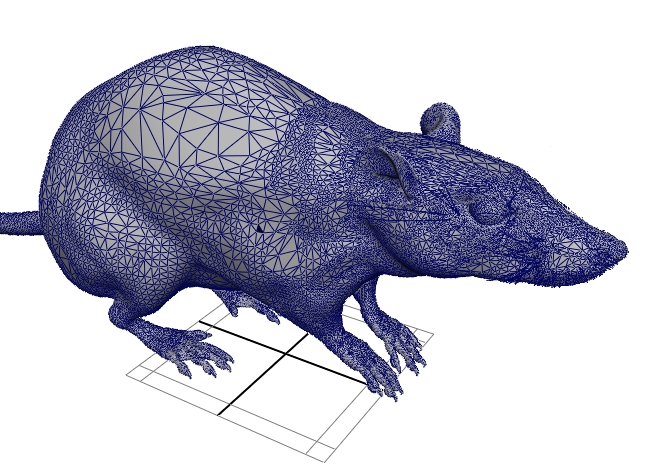 Photo d'un modèle (statique)
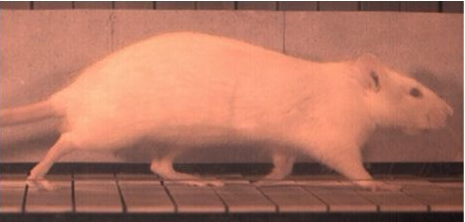
Capture vidéo d'un animal en mouvement Un modèle maillé (statique) correspondant
(Images : Lionel Revéret)

Responsables

Lionel Revéret Franck Hétroy
LJK/EVASION LJK/EVASION
E-mail : Lionel.Reveret@inrialpes.fr E-mail : Franck.Hetroy@imag.fr
Tél. : 04 76 61 52 36 Tél. : 04 76 61 55 04

Contexte

Dans le cadre du projet ANR Kameleon, réunissant EVASION, le Muséum National d'Histoire Naturelle, le Laboratoire de Neurobiologie des Réseaux Sensorimoteurs de Paris et le Laboratoire de Physiologie et Biomécanique de l'Exercice Musculaire de Rennes, nous disposons de séquences vidéos d'animaux en mouvement. Dans un but à long terme de prédiction du mouvement du squelette à partir de celui de l'enveloppe externe (la peau), nous souhaitons travailler sur une représentation virtuelle de ces animations. L'objectif de ce stage est de créer cette représentation, en accordant une attention particulière au maintien de la cohérence temporelle de caractéristiques géométriques. Il nécessite des compétences à la fois en informatique graphique et animation, en vision par ordinateur et en géométrie appliquée.

Objectifs

Les travaux à réaliser lors de ce stage ont trait à la fois à la vision par ordinateur et à la géométrie appliquée (geometry processing).

D'une part, il s'agira de déduire un flux de points 3D à partir de séquences vidéos calibrées par calcul de stéréo dense. On s'appuiera notamment sur les travaux de Zhang et al. qui s'affranchissent de la contrainte d'apparaiement dans le plan fronto-parallèle [1,2]. Les algorithmes présentés dans [1] utilisent la lumière structurée. Ce procédé n'est techniquement pas envisageable pour les rongeurs : il faudra donc étudier le remplacement de la lumière structurée par une recherche de cohérence spatiale dans la texture de la fourrure.

D'autre part, il s'agira de développer une méthode de reconstruction de surface (par exemple maillage) animée à partir de ce flux de points 3D, en s'attachant à conserver une cohérence temporelle de la reconstruction d'une frame à la suivante. Pour cela, le travail pourra commencer par une double étude bibliographique :

  1. des méthodes existantes de reconstruction statique d'une surface à partir d'un nuage de points ;
  2. des méthodes existantes de détection/calcul de caractéristiques géométriques sur des surfaces ou des nuages de points ;

Les premières sont nombreuses [3,4,5]. Malheureusement, elles ne reconstruisent qu'une surface statique, et pour peu que cette surface soit légèrement modifiée, la reconstruction peut devenir complètement différente. Dans le domaine de la simulation numérique ont été développées des méthodes de création de maillages dynamiques, qui suivent l'évolution d'une surface en mouvement, à partir d'un maillage de la surface à l'état initial [6]. Cependant, ces techniques nécessitent une première reconstruction de surface statique par un maillage très dense, et les caractéristiques géométriques de la surface ne sont pas particulièrement suivies. Les plus étudiées de ces caractéristiques, telles les courbures [7], ne sont pas forcément conservées lors d'une animation. Nous cherchons en effet à détecter des caractéristiques géométriques invariantes au cours du temps. Les étranglements [8] ou les sphériques ou variétés harmoniques [9,10] sont des voies plus prometteuses qu'on pourra analyser. Une autre direction de recherche possible concerne la segmentation du flux de points en zones (spatiales) évoluant de manière quasi-rigide dans le temps [11,12].

Le stagiaire développera en C/C++ et utilisera la bibliothèque Graphite développée à l'INRIA Lorraine.

Mots-clés : reconstruction, représentation géométrique, cohérence temporelle.

Références

  1. L. Zhang, N. Snavely, B. Curless, S. Seitz. Spacetime Faces: High-Resolution Capture for Modeling and Animation. SIGGRAPH, 2004.
  2. J. Davis, D. Nehab, R. Ramamoothi, S. Rusinkiewicz. Spacetime Stereo: A Unifying Framework for Depth from Triangulation. IEEE Transactions on Pattern Analysis and Machine Intelligence (PAMI), 2005.
  3. P. Alliez, D. Cohen-Steiner, Y. Tong, M. Desbrun. Voronoi-based Variational Reconstruction of Unoriented Point Sets. Symposium on Geometry Processing, 2007.
  4. T.K. Dey. Curve and Surface Reconstruction: Algorithms with Mathematical Analysis. Cambridge University Press, 2007.
  5. A. Sharf, T. Lewiner, A. Shamir, L. Kobbelt, D. Cohen-Or. Competing Fronts for Coarse-to-fine Surface Reconstruction. Eurographics, 2006.
  6. X. Jiao, A. Colombi, X. Ni, J. Hart. Anisotropic Mesh Adaptation for Evolving Triangulated Surfaces. International Meshing Roundtable, 2006.
  7. D. Cohen-Steiner, J.-M. Morvan. Second Fundamental Measure of Geometric Sets and Local Approximation of Curvatures. Journal of Differential Geometry, 2006.
  8. F. Hétroy, D. Attali. Detection of Constrictions on Closed Polyhedral Surfaces. Eurographics-IEEE TCVG Visualization Symposium, 2003.
  9. M. Mousa, R. Chaine, S. Akkouche, E. Galin. Efficient Spherical Harmonics Representation of 3D Objects. Pacific Graphics, 2007.
  10. B. Vallet, B. Lévy. Spectral Geometry Processing with Manifold Harmonics. Research report, 2007.
  11. A. Y. Ng, M. I. Jordan, Y. Weiss. On Spectral Clustering: Analysis and an algorithm. NIPS, 2001.
  12. O. Sorkine, M. Alexa. As-Rigid-as-Possible Surface Modeling. Symposium on Geometry Processing 2007.