Sujet de M2R IVR 2005-2006
D'un squelette géométrique à un squelette d'animation
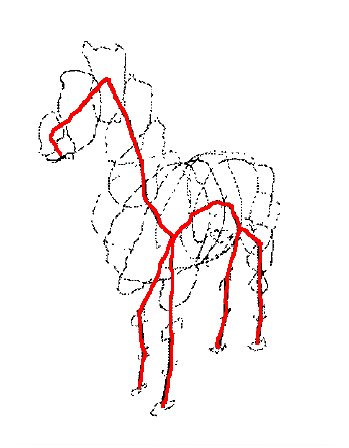 |
 |
| Squelette géométrique |
Squelette d'animation |
Responsables
| Franck Hétroy | Francis Lazarus |
| GRAVIR/EVASION | LIS |
| E-mail : Franck.Hetroy@imag.fr | E-mail : Francis.Lazarus@lis.inpg.fr |
| Tél. : 04 76 61 55 04 | Tél. : 04 76 82 64 67 |
Résumé
Afin d'animer un personnage ou un animal virtuel en trois dimensions (représenté sous forme
de surface maillée), la méthode la plus couramment utilisée consiste à créer une
représentation hiérarchique des articulations principales, appelée squelette d'animation.
Chaque articulation du squelette peut être déplacée individuellemment ; le squelette est
alors déformé par cinématique directe ou inverse, et le modèle 3D de l'enveloppe externe est
ensuite lui-même déformé autour de celui-ci. L'utilisation du squelette améliore et
simplifie considérablement la génération d'animations de modèles 3D, mais souffre de
plusieurs limitations. La principale concerne la construction du
squelette : il n'existe actuellement aucune méthode de calcul automatique d'un squelette
pour l'animation, et la pose de celui-ci se révèle être une tâche longue et fastidieuse.
En fait, les techniques existantes de construction automatique d'un squelette
géométrique ne conviennent pas réellement au domaine de l'animation, car les squelettes ne
sont pas positionnés de manière anatomiquement adéquate, ce qui génère des
animations non réalistes.
Parmi les squelettes géométriques proposés, ceux représentés sous forme de graphes topologiques noeuds-arêtes [2] sont néanmoins intéressants, car leur structure se rapproche de celle d'un squelette d'animation. Il convient néanmoins de choisir de manière astucieuse la définition d'un tel graphe, afin que d'une part il ne soit pas trop complexe pour les modèles étudiés, et que d'autre part sa structure se rapproche le plus possible de celle d'un squelette d'animation. Nous pensons qu'un graphe de Reeb défini par rapport à la fonction de Morse moyennée proposée dans [5] peut convenir pour résoudre ce problème. Les trois problèmes qui restent alors posés sont :
- la modification du graphe (ajoût/suppression de noeuds et d'arêtes) pour correspondre au graphe du squelette d'animation ;
- le plongement de ce graphe dans R³ pour que le squelette soit géométriquement placé au même endroit que le squelette d'animation ;
- la définition des hiérarchies entre les noeuds du graphe.
Le but de ce stage est de transformer un tel squelette géométrique en un squelette
d'animation, de manière automatique ou semi-automatique. L'équipe EVASION dispose de
nombreux squelettes d'animation de référence, créés à la main pour des modèles de
quadrupèdes [6]. Le squelette géométrique de départ correspond à un plongement dans R³ d'un
graphe de Reeb, calculé en temps O(n log n) [3]. Le plongement proposé au départ est celui
décrit dans [4].
Le stagiaire développera en C/C++ et utilisera la bibliothèque CGAL. L'interface de
visualisation sera réalisée sous OpenGL. Les programmes écrits permettront éventuellement
la création d'un plugin Maya [1].
Mots-clés : squelette, animation, graphe de Reeb, fonction de Morse, comparaison
de graphes.
Objectifs
- Implémenter la fonction de Morse proposée dans [5] et évaluer son efficacité pour la construction d'un graphe de Reeb dont la structure se rapproche de celle d'un squelette d'animation.
- Proposer un plongement judicieux dans R^3 du graphe de Reeb de cette fonction pour les modèle de quadrupèdes fournis.
- Comparer les squelettes géométriques ainsi générés et les squelettes d'animation créés manuellement, et proposer une classification des divergences.
- Proposer un algorithme de conversion automatique ou semi-automatique d'un squelette géométrique en un squelette d'animation, basé sur les observations faites. On pourra éventuellement proposer une liste de règles autorisées pour modifier manuellement un squelette géométrique. Il faudra également faire attention à bien rendre le squelette hiérarchique.
Références
- Alias|Wavefront. Maya software. http://www.alias.com/.
- S. Biasotti, S. Marini, M. Mortara, G. Patané. An Overview on Properties and Efficacy of Topological Skeletons in Shape Modelling. In Shape Modeling International (SMI), 2003.
- K. Cole-McLaughlin, H. Edelsbrunner, J. Harer, V. Natarajan, V. Pascucci. Loops in Reeb Graphs of 2-Manifolds. In Symposium on Computational Geometry (SoCG), 2003.
- F. Lazarus, A. Verroust. Level Set Diagrams of Polyhedral Objects. In Solid Modeling (SM), 1999.
- X. Ni, M. Garland, J. C. Hart. Fair Morse Functions for Extracting the Topological Structure of a Surface Mesh. In SIGGRAPH, 2004.
- L. Revéret, L. Favreau, C. Depraz, M.P. Cani. Morphable model of quadrupeds skeletons for animating 3D animals. In Symposium on Computer Animation (SCA), 2005.